Puzzle‐Friendliness Sifat Tambahan Ketiga
Sifat 3: Puzzle‐Friendliness
Sifat tambahan selanjutnya adalah Puzzle‐Friendliness. Teknisnya kita akan mencari tahu persyaratan apa yang dibutuhkan agar bisa dipergunakan. Selanjutnya memberikan ilustrasi mengapa sifat puzzle-friendliness ini cukup berguna.
Puzzle‐friendliness
Sebuah fungsi hash H dikatakan memiliki sifat puzzle-friendliness jika setiap kemungkinan output n-bit bernilai y, dan jika k dipilih dari distribusi dengan min-entropi tinggi, maka tidak bisa untuk menemukan x, sehingga H (k ‖ x) = y pada waktu yang secara signifikan kurang dari 2n.
Artinya adalah, jika seseorang ingin menargetkan fungsi hash agar bisa keluar di beberapa nilai output tertentu y, maka ada bagian dari input yang dipilih dengan acak itu menjadi sangat sulit untuk bisa menemukan nilai lain yang bisa sama persis seperti target.
Aplikasi: Search puzzle.
Sekarang kita coba untuk mempertimbangkan sebuah aplikasi yang menggambarkan kegunaan sifat ini. Dalam aplikasi ini, kita akan coba membangun sebuah pencari puzzle. Artinya sebuah puzzle disini adalah sebuah masalah matematis yang membutuhkan ruang besar untuk bisa menemukan solusinya. Secara khusus, pencari puzzle ini tidak memiliki shortcut (jalan pintas). Artinya, tidak ada cara untuk menemukan solusi valid selain mencari ruang besar itu.
Aplikasi Pencari puzzle. umumnya akan terdiri dari:
⦁ fungsi hash, H,
⦁ nilai, id (yang kita sebut puzzle-ID), dipilih dari distribusi min-entropi tinggi
⦁ dan target yang ditetapkan Y
Solusi untuk teka-teki ini adalah nilai x, sehingga H (id ‖ x) ∈ Y
Jika H memiliki output n-bit, maka dapat mengambil dari nilai-nilai 2n. Dalam memecahkan teka-teki butuh untuk bisa menemukan sebuah input. Sehingga output bisa termasuk dalam set Y, yang biasanya berukuran lebih kecil dari semua himpunan output lainnya. Ukuran Y ditentukan dari seberapa rumit puzzle tersebut. Sementara, jika Y adalah semua himpunan string n-bit yang tidak terlalu rumit, sedangkan Y hanya memiliki 1 elemen puzzle, maka menjadi cukup sulit.
Fakta bahwa id puzzle dengan min-entropy tinggi memasikan agar tidak ada shortcut atau jalan pintas apapun. Sebaliknya, jika nilai tertentu dari ID memungkinkan, maka seseorang berpeluang untuk melakukan kecurangan. Misalnya melakukan pra komputansi memecahkan puzzle dengan menggunakan ID tersebut.
Jika pencari puzzle itu bersifat puzzle-friendliness, implikasinya tidak ada pemecahan puzzle yang jauh lebih baik daripada menggunakan nilai acak x. Dan, kita bisa membuat sebuah puzzle yang sukar untuk dipecahkan dengan cara ini. Selama kita bisa melakukan generate ID puzzle secara acak. Ide tentang hal ini selanjutnya dipergunakan dalam proses penambangan bitcoin, yang juga dilakukan dengan komputansi puzzle.
SHA-256
Ada cukup banyak fungsi hash yang telah ada. Namun pada Bitcoin, fungsi hash yang satu ini menjadi yang utama dan cukup baik untuk digunakan. Fungsi ini disebut dengan SHA-256. Hash umumnya disajikan dalam bentuk bilangan hexadecimal, yaitu kombinasi antara angka 0-9 dengan huruf a hingga f.
Perlu diingat bahwa kita memerlukan fungsi hash untuk bisa bekerja pada input dengan panjang tertentu, tetap. Ada sebuah metode umum yang bisa mengubahnya menjadi sebuah fungsi hash yang bisa bekerja pada panjang input yang berubah-ubah. Metode itu disebut Merkle-Damgard transform. SHA-256 adalah salah satu dari sekian banyak fungsi hash yang digunakan dalam metode ini. Dalam terminologi secara umum, panjang yang tetap dari sifat fungsi hash collision-resistant disebut dengan compression-function. Dan hal ini telah terbukti. Sehingga jika compression-function tersebut adalah collision-resistant, maka secara keseluruhan fungsi hash adalah collision-resistant juga.
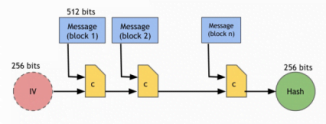
Proses Merkle-Damgard cukup sederhana. Compression-function mengambil panjang input m dan menghasilkan output yang lebih pendek n. Input ke fungsi hash tersebut, dapat dari berbegai ukuran, kemudian dibagi menjadi blok-blok dengan ukuran panjang m-n. Proses kerjanya melalui setiap blok bersama dengan output blok sebelumnya kedalam compression-function. Perhatikan bahwa panjang input akan menjadi (m-n)+n = m, yang merupakan panjang input sebagai fungsi untuk compression-function tersebut. Jika blok tersebut adalah blok pertama, tentu tidak ada output blok sebelumnya. Dan jika menggunakan intialization Vector, jumlah tersebut digunakan kembali untuk memanggil fungsi hash.
SHA-256 menggunakan compression-function dengan mengambil input 768-bit, dan menghasilkan output 256-bit. Ukuran blok adalah 512 bit.
Pada gambar itu, SHA-256 menggunakan Merkle-Damgard untuk mengubah panjang yang tetap dari collision-resistant compression-functoin menjadi fungsi hash, yang bisa menerima input berbagai ukuran.
Dengan demikian, kita telah membahas tentang fungsi hash, beberapa sifat khusus tambahan fungsi hash kriptografi, aplikasi dari sifat fungsi hash tersebut, dan juga fungsi hash tertentu yang digunakan dalam Bitcoin. Bahasan selanjutnya akan mengarah pada fungsi hash dengan struktur data yang lebih rumit yang digunakan dalam sistem Bitcoin.
Leave a Reply
You must be logged in to post a comment.